深度学习系列第二篇 — 深度神经网络
上一节学习的向前传播算法是一种线性模型,全连接神经网络和单层神经网络模型都只能处理线性问题,这具有相当大的局限性。而深度学习要强调的是非线性。
激活函数去线性化
如下图,如果我们将每一个神经元的输出通过一个非线性函数,那么这个神经网络模型就不再是线性的了,而这个非线性函数就是激活函数,也实现了我们对神经元的去线性化。
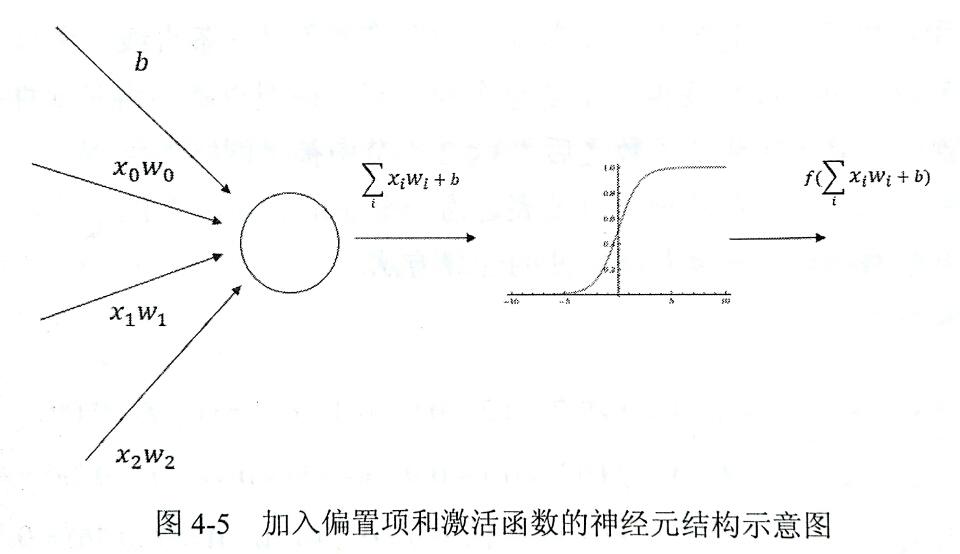
下面列举了三个常用激活函数
- ReLU 函数
- sigmoid 函数
- tanh 函数
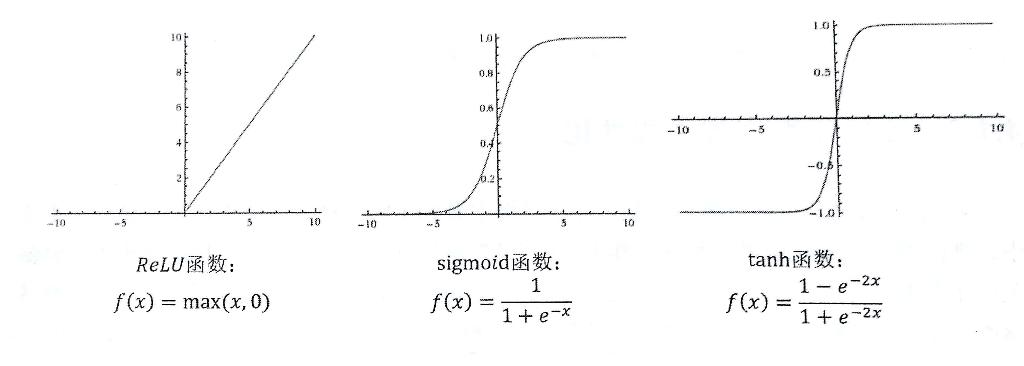
tf 中也提供了这几种不同的非线性激活函数。
tf.nn.relu(tf.matmul(x, w1) + biases1)
通过对 x 的加权增加偏置项,再在外层加上激活函数,实现神经元的非线性化。
损失函数
损失函数用来衡量预测值与真实值之间的不一致程度,是一个非负实值函数,损失函数越小,证明模型预测的越准确。
交叉熵可以用来衡量两个概率分布之间的距离,是分类问题中使用比较光的一种损失函数。对于两个概率分布 p 和 q,表示交叉熵如下:
$$H(p,q)=-\sum_{x}p(x)log q(x)$$
将神经网络向前传播得到的结果变成概率分布使用 Softmax 回归,它可以作为一个算法来优化分类结果。假设神经网络的输出值为 y1,y2,...yn,那么 Softmax 回归处理的输出为:
$$softmax(y)i=y_i’=\frac{e^{yi}}{\sum{j=1}^ne^{yj}}$$
如下图通过 Softmax 层将神经网络的输出变成一个概率分布。
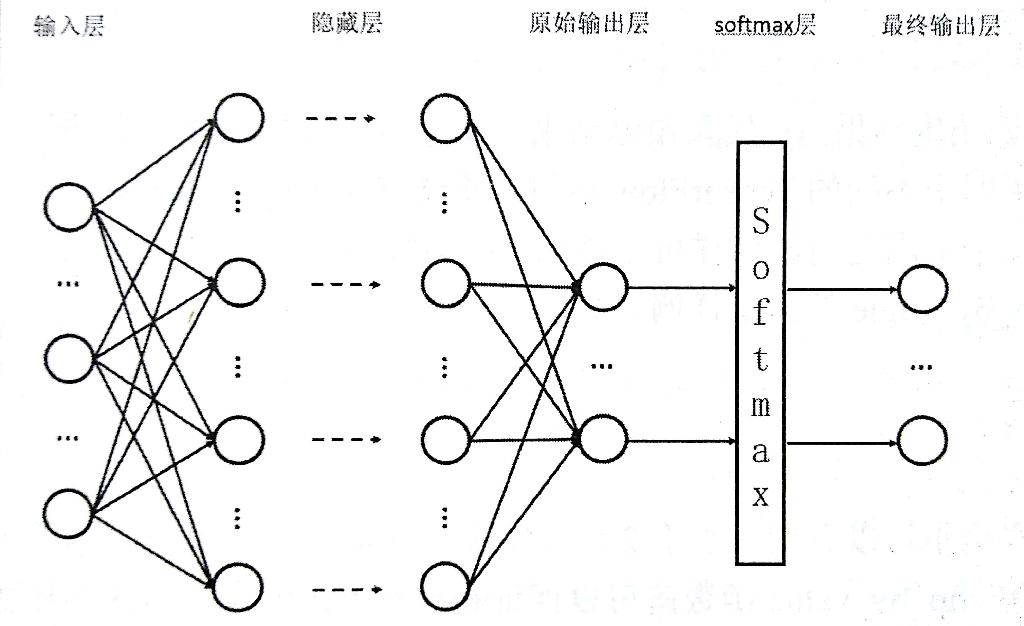
交叉熵一般会与 Softmax 回归一起使用,tf 对这两个功能提供了封装提供函数 tf.nn.softmax_cross_entropy_with_logits。
对于回归问题区别与分类问题,需要预测的是一个任意实数,最常使用的损失函数是均方误差 MSE,定义如下:
$$MSE(y,y’)=\frac{\sum_{i=1}^n(y_i-y_i’)^2}{n}$$
反向传播算法
反向传播算法是训练神经网络的核心算法,它可以根据定义好的损失函数优化神经网络的参数值,是神经网络模型的损失函数达到一个较小的值。
梯度下降算法是最常用的神经网络优化方法,假设用 θ 表示神经网络的参数, J(θ) 表示给定参数下的取值,梯度下降算法会迭代式的更新 θ,让迭代朝着损失最小的方向更新。梯度通过求偏导的方式计算,梯度为 $$\frac{∂}{∂θ}J(θ)$$ 然后定义一个学习率 η。参数更新公式如下:$$θ_{n+1}=θ_n-η\frac{∂}{∂θ_n}J(θ_n)$$
优化过程分为两步:
- 通过向前传播算法得到预测值,将预测值与真实值之间对比差距。
- 通过反向传播算法计算损失函数对每一个参数的梯度,根据梯度和学习率是梯度下降算法更新每一个参数。
为了降低计算量和加速训练过程,可以使用随机梯度下降算法,选取一部分数据进行训练。
学习率的设置可以通过指数衰减法,逐步减小学习率,可以在开始时快速得到一个较优解,然后减小学习率,使后模型的训练更加稳定。tf 提供了tf.train.exponential_decay 函数实现指数衰减学习率, 每一轮优化的学习率 = 初始学习率 * 衰减系数 ^ (学习步数 / 衰减速度)
过拟合问题
通过损失函数优化模型参数的时候,并不是让模型尽量的模拟训练数据的行为,而是通过训练数据对未知数据给出判断,当一个模型能完美契合训练数据的时候,损失函数为0,但是无法对未知数据做出可靠的判断,这就是过拟合。
避免过拟合的常用方法是正则化,就是在损失函数中加入刻画模型复杂度的指标,我们对模型的优化则变为 $$J(θ)+λR(w)$$ 其中 R(w) 刻画的是模型的复杂程度,λ 表示模型复杂损失在总损失中的比例。下面是常用的两种正则化函数:
L1正则化:会让参数变得稀疏,公式不可导
$$R(w) = \Vertw\Vert_1 = \sum_i|w_i|$$
L2正则化:不会让参数变得稀疏,公式可导
$$R(w) = \Vertw\Vert_2^2 = \sum_i|w_i^2|$$
在实际使用中会将 L1 正则化和 L2 正则化同时使用:
$$R(w) = \sum_iα|w_i|+(1-α)w_i^2$$
滑动平均模型
在采用随机梯度下降算法训练神经网络时,使用平均滑动模型可以在大部分情况下提高模型在测试数据上的表现。在 tf 中提供了 tf.train.ExponentialMovingAverage 来实现这个模型,通过设置一个衰减率来初始化,在其中维护一个影子变量,可以控制模型的更新速度。影子变量值 = 衰减率 * 影子变量值 + (1 - 衰减率) * 待更新变量,为了让模型前期更新比较快,还提供了 num_updates 参数,每次使用的衰减率为:
$$min(decay,\frac{1+numupdates}{10+numupdates})$$
附 mathjax 语法教程:http://blog.csdn.net/u010945683/article/details/46757757
本章结束~