深度学习系列第五篇 — 卷积神经网络

发表于 2017-11-18

这篇例子是学习莫烦PYTHON 视频教程整理的学习笔记。

卷积神经网络包含如下几层：

输入层
卷积层（卷积层的结构 + 向前传播算法） =>> （过滤器或内核）（用来提取特征,每一层会将图层变厚）
池化层（用来采样，稀疏参数，每一层会将图层变瘦）
全连接层（将前两层提取的图像特征使用全连接层完成分类任务）
Softmax 层（主要处理分类，得到不同种类的概率分布情况）

cnn

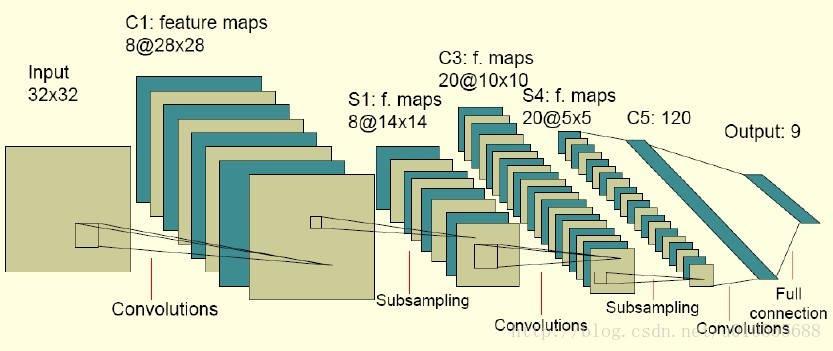
首先我们将如下包导入，这次练习是通过 Tensorflow 提供的 MNIST 数据集进行训练，识别手写数字。

import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data

# 下载或加载数据
mnist = input_data.read_data_sets("MNIST_data", one_hot=True)

Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz

def weight_variable(shape):
    inital = tf.truncated_normal(shape, stddev=0.1)
    return tf.Variable(inital)


def bias_variable(shape):
    inital = tf.constant(0.1, shape=shape)
    return tf.Variable(inital)

def add_layer(inputs, in_size, out_size, activation_function=None):
    # 在生成初始参数时，随机变量(normal distribution)会比全部为0要好很多
    # 所以我们这里的weights为一个in_size行, out_size列的随机变量矩阵。
    weights = tf.Variable(tf.random_normal([in_size, out_size]))
    # biases的推荐值不为0，所以我们这里是在0向量的基础上又加了0.1
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    wx_plus_b = tf.matmul(inputs, weights) + biases
    if activation_function is None:
        outputs = wx_plus_b
    else:
        outputs = activation_function(wx_plus_b)
    return outputs

def compute_accuracy(v_xs, v_ys):
    global prediction
    y_pre = sess.run(prediction, feed_dict={xs: v_xs, keep_drop: 1})
    correct_prediction = tf.equal(tf.argmax(y_pre,1), tf.argmax(v_ys,1))
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    result = sess.run(accuracy, feed_dict={xs: v_xs, ys: v_ys, keep_drop: 1})
    return result

def conv2d(x, w):
    # stride [1, x_movement, y_movement, 1]
    # Must have strides[0] = strides[4] = 1
    return tf.nn.conv2d(x, w, strides=[1,1,1,1], padding='SAME')

def max_pool_2x2(x):
    # stride [1, x_movement, y_movement, 1]
    return tf.nn.max_pool(x, ksize=[1,2,2,1], strides=[1,2,2,1], padding='SAME')

xs = tf.placeholder(tf.float32, [None, 784])  # 28 * 28
ys = tf.placeholder(tf.float32, [None, 10])
keep_drop = tf.placeholder(tf.float32)
x_image = tf.reshape(xs, [-1, 28, 28, 1])
# print x_image.shape  # [n_sample, 28, 28, 1]

# conv1 layer #
w_conv1 = weight_variable([5,5,1,32])  # patch 5 x 5, in size 1, out size 32
b_conv1 = bias_variable([32])
h_conv1 = tf.nn.relu(conv2d(x_image, w_conv1) + b_conv1)  # output size 28 x 28 x 32
h_pool1 = max_pool_2x2(h_conv1)  # output size 14 x 14 x 32

# conv2 layer #
w_conv2 = weight_variable([5,5,32,64])  # patch 5 x 5, in size 32, out size 64
b_conv2 = bias_variable([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, w_conv2) + b_conv2)  # output size 14 x 14 x 64
h_pool2 = max_pool_2x2(h_conv2)  # output size 7 x 7 x 64

# func1 layer #
w_fc1 = weight_variable([7 * 7 * 64, 1024])
b_fc1 = bias_variable([1024])
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])  # [n_sample, 7, 7 64]  -> [n_sample, 7*7*64]
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, w_fc1) + b_fc1)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_drop)

# func2 layer #
w_fc2 = weight_variable([1024, 10])
b_fc2 = bias_variable([10])

通过使用 softmax 分类器输出分类

1	prediction = tf.nn.softmax(tf.matmul(h_fc1_drop, w_fc2) + b_fc2)

loss函数（即最优化目标函数）选用交叉熵函数。交叉熵用来衡量预测值和真实值的相似程度，如果完全相同，它们的交叉熵等于零。

1	cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf.log(prediction), reduction_indices=[1]))

通过使用 AdamOptimizer 优化器进行优化，使 cross_entropy 最小

1	train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

下面开始训练，通过两千次的训练，每次抽样 100 条数据，每 100 次训练完验证一下预测的准确率

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())

    for i in range(1, 2001):
        batch_xs, batch_ys = mnist.train.next_batch(100)
        sess.run(train_step, feed_dict={xs: batch_xs, ys: batch_ys, keep_drop: 0.5})
        if i % 100 == 0:
            print i, compute_accuracy(
                mnist.test.images[:1000], mnist.test.labels[:1000])

print "end!"

训练结果：