码力欧

深度学习系列第四篇 — 神经反向传播

发表于 2017-09-28

反向传播算法

反向传播算法 - 维基百科

反向传播是一种与最优化方法结合使用的，用来训练人工神经网络的常用方法。通过计算所有权值的损失函数梯度，反馈给最优化方法，用来更新权值以最小化损失函数。

反向传播算法分成两个阶段：激励传播和权值更新

激励传播：将输入值送入网络，活的激励响应，验证结果求差，从而获得响应误差。
权重更新：将输入的激励和响应误差相乘，获得权重的梯度，将梯度乘一个比例后取反加到权重上。

训练的过程就是不断的重复这两个阶段，直到获得满意的预测准确率。

深度学习系列第二篇 — 深度神经网络

发表于 2017-09-25

上一节学习的向前传播算法是一种线性模型，全连接神经网络和单层神经网络模型都只能处理线性问题，这具有相当大的局限性。而深度学习要强调的是非线性。

激活函数去线性化

如下图，如果我们将每一个神经元的输出通过一个非线性函数，那么这个神经网络模型就不再是线性的了，而这个非线性函数就是激活函数，也实现了我们对神经元的去线性化。

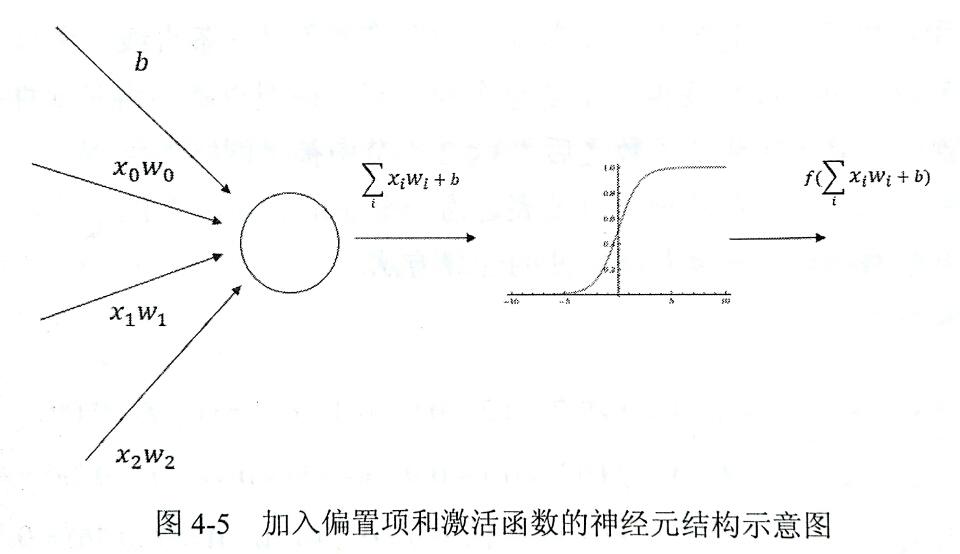
激活函数去线性化

下面列举了三个常用激活函数

ReLU 函数
sigmoid 函数
tanh 函数

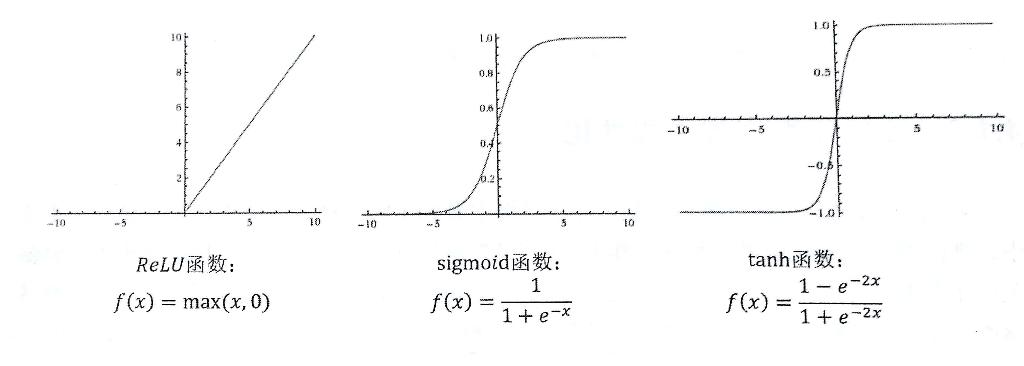
激活函数去线性化

tf 中也提供了这几种不同的非线性激活函数。

tf.nn.relu(tf.matmul(x, w1) + biases1)

通过对 x 的加权增加偏置项，再在外层加上激活函数，实现神经元的非线性化。

损失函数

损失函数用来衡量预测值与真实值之间的不一致程度，是一个非负实值函数，损失函数越小，证明模型预测的越准确。

交叉熵可以用来衡量两个概率分布之间的距离，是分类问题中使用比较光的一种损失函数。对于两个概率分布 p 和 q，表示交叉熵如下：

$$H(p,q)=-\sum_{x}p(x)log q(x)$$

将神经网络向前传播得到的结果变成概率分布使用 Softmax 回归，它可以作为一个算法来优化分类结果。假设神经网络的输出值为 y1,y2,...yn，那么 Softmax 回归处理的输出为：

$$softmax(y)i=y_i’=\frac{e^{yi}}{\sum{j=1}^ne^{yj}}$$

如下图通过 Softmax 层将神经网络的输出变成一个概率分布。

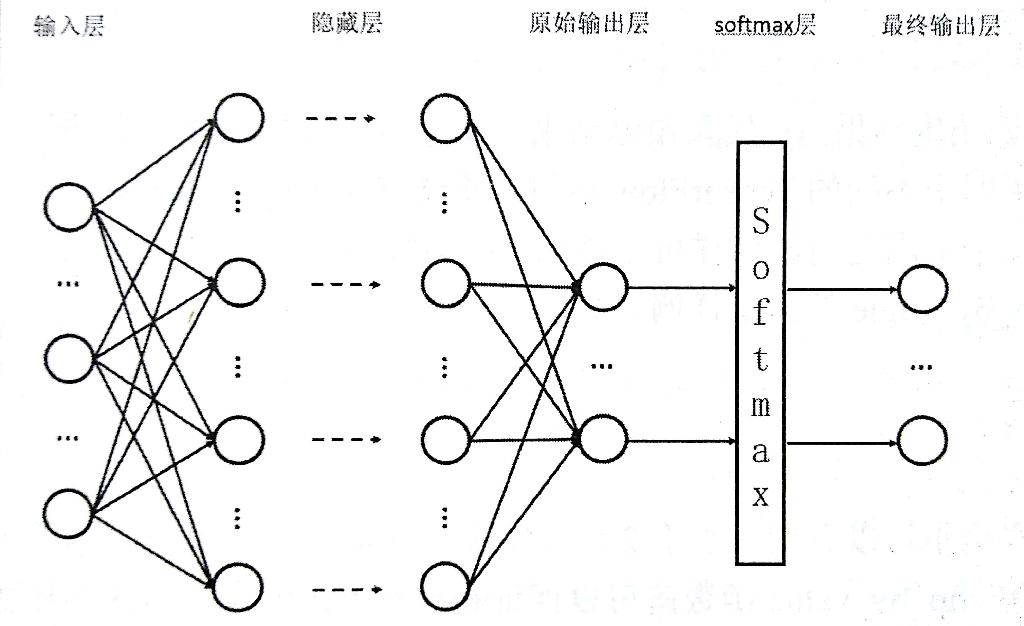
Softmax

交叉熵一般会与 Softmax 回归一起使用，tf 对这两个功能提供了封装提供函数 tf.nn.softmax_cross_entropy_with_logits。

对于回归问题区别与分类问题，需要预测的是一个任意实数，最常使用的损失函数是均方误差 MSE,定义如下：

$$MSE(y,y’)=\frac{\sum_{i=1}^n(y_i-y_i’)^2}{n}$$

反向传播算法

反向传播算法是训练神经网络的核心算法，它可以根据定义好的损失函数优化神经网络的参数值，是神经网络模型的损失函数达到一个较小的值。

梯度下降算法是最常用的神经网络优化方法，假设用 θ 表示神经网络的参数， J(θ) 表示给定参数下的取值，梯度下降算法会迭代式的更新 θ，让迭代朝着损失最小的方向更新。梯度通过求偏导的方式计算，梯度为 $$\frac{∂}{∂θ}J(θ)$$ 然后定义一个学习率 η。参数更新公式如下：$$θ_{n+1}=θ_n-η\frac{∂}{∂θ_n}J(θ_n)$$

优化过程分为两步：

通过向前传播算法得到预测值，将预测值与真实值之间对比差距。
通过反向传播算法计算损失函数对每一个参数的梯度，根据梯度和学习率是梯度下降算法更新每一个参数。

为了降低计算量和加速训练过程，可以使用随机梯度下降算法，选取一部分数据进行训练。

学习率的设置可以通过指数衰减法，逐步减小学习率，可以在开始时快速得到一个较优解，然后减小学习率，使后模型的训练更加稳定。tf 提供了tf.train.exponential_decay 函数实现指数衰减学习率， 每一轮优化的学习率 = 初始学习率 * 衰减系数 ^ (学习步数 / 衰减速度)

过拟合问题

通过损失函数优化模型参数的时候，并不是让模型尽量的模拟训练数据的行为，而是通过训练数据对未知数据给出判断，当一个模型能完美契合训练数据的时候，损失函数为0，但是无法对未知数据做出可靠的判断，这就是过拟合。

避免过拟合的常用方法是正则化，就是在损失函数中加入刻画模型复杂度的指标，我们对模型的优化则变为 $$J(θ)+λR(w)$$ 其中 R(w) 刻画的是模型的复杂程度，λ 表示模型复杂损失在总损失中的比例。下面是常用的两种正则化函数：

L1正则化：会让参数变得稀疏，公式不可导

$$R(w) = \Vertw\Vert_1 = \sum_i|w_i|$$

L2正则化：不会让参数变得稀疏，公式可导

$$R(w) = \Vertw\Vert_2^2 = \sum_i|w_i^2|$$

在实际使用中会将 L1 正则化和 L2 正则化同时使用：

$$R(w) = \sum_iα|w_i|+(1-α)w_i^2$$

滑动平均模型

在采用随机梯度下降算法训练神经网络时，使用平均滑动模型可以在大部分情况下提高模型在测试数据上的表现。在 tf 中提供了 tf.train.ExponentialMovingAverage 来实现这个模型，通过设置一个衰减率来初始化，在其中维护一个影子变量，可以控制模型的更新速度。
影子变量值 = 衰减率 * 影子变量值 + (1 - 衰减率) * 待更新变量，为了让模型前期更新比较快，还提供了 num_updates 参数，每次使用的衰减率为：

$$min(decay,\frac{1+numupdates}{10+numupdates})$$

附 mathjax 语法教程：http://blog.csdn.net/u010945683/article/details/46757757

本章结束～

深度学习系列第一篇 — 入门

发表于 2017-09-21

这篇文章是学习人工智能的笔记，首先抛出下面一个问题。

人工智能、机器学习和深度学习之间的关系？

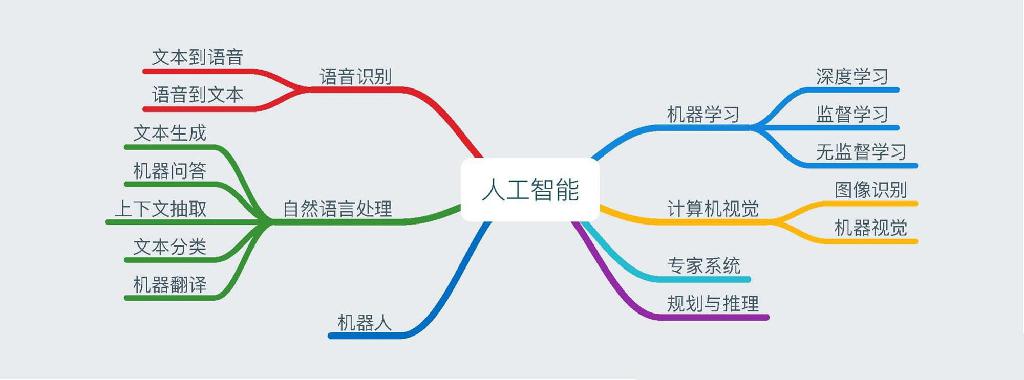
三者之间的联系

从图中可以看出人工智能概念的范围更广，机器学习是其中的一个子集，而深度学习又是机器学习中的一个子集。

深度学习的应用领域在计算机视觉、语音识别、自然语言处理和人机博弈方面比基于数理统计的机器学习会有更高的准确度。这里主要是做深度学习方面的学习笔记。

深度学习的发展历程

深度发学习是深度神经网络的代名词，其起源于上世纪，只是在这几年开始火起来。

早期的神经网络模型类似于放生机器学习，由人类大脑的神经元演化出的神经元模型，见下图（图摘自《TensorFlow 实战Google深度学习框架》）：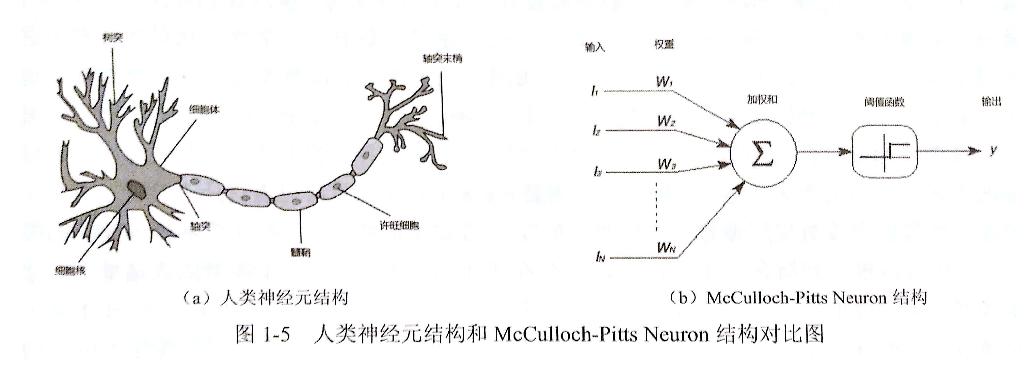
对比图

后面出现了感知机模型、分布式知识表达和神经网络反向传播算法，再到后来的卷积神经网络、循环神经网络和 LSTM 模型。

在神经网络发展的同时，传统机器学习算法的研究也在不断发展，上世纪 90 年代末逐步超越了神经网络，在当时相比之下传统机器学习算法有更好的识别准确率，而神经网络由于数据量和计算能力的限制发展比较困难。到了最近几年，由于云计算、GPU、大数据等的出现，为神经网络的发展做好了铺垫，AI 开始了一个新的时代。从自身出发，高中设立的一个比较模糊的梦想是参与到人工智能的研发当中去，所以大学学了计算机，当梦想与时代的发展有了一个交点，梦想的实现变得更加触手可及。

下面一张图表是对比主流深度学习开源工具（图摘自《TensorFlow 实战Google深度学习框架》）

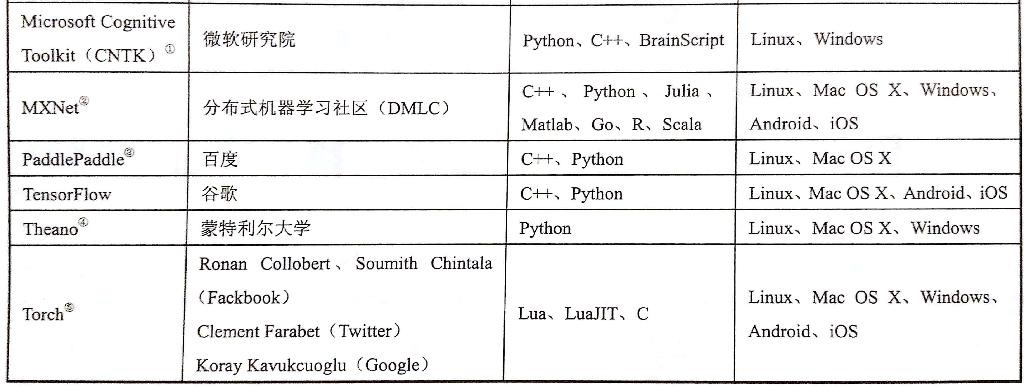
目前我听说的比较多的两个开源工具是 Caffe 和 TensorFlow，然后去看了下 Github 关注量，前者 20.1k 后者 69.3k，TensorFlow 应该是目前最火的一个深度学习框架了吧。这篇文章包括后面的文章都会去记录 TensorFlow 的学习过程，下面的内容是介绍 TensorFlow 的基础概念，介绍中我尽量避免加入代码，因为目前 TensorFlow 更新比较快，发现好多写法在新的版本中不再被支持。

TensorFlow 学起来

TensorFlow 有两个重要概念 Tensor （张量）和 Flow（流），Tensor 表名的是数据结构，Flow 提现的是计算模型。

PS:以下将 TensorFlow 简称为 tf

tf 计算模型 — 计算图

tf 通过计算图来表述计算的编程系统，其中的每个节点表示一个计算，不同点之间的连接表达依赖关系。下面几行代码表达一下：

import tensorflow as tf
a = tf.constant([1.0, 2.0], name='a')
b = tf.constant([2.0, 3.0], name='b')
result = a + b

上面的代码在计算图中会有 a、b、a + b三个节点。tf 默认会有一个全局的计算图，也可以生成新的计算图，不同计算图之间不会共享张量和运算。

计算图中可以通过集合的方式管理不同的资源，这些资源可以是张量、变量或者队列资源等。

tf 数据模型 — 张量

张量是 tf 管理和表示数据的形式，可以简单理解为多维数组。零阶张量表示标量，就是一个数；一阶张量是一个一维数组；n 阶张量是一个 n 维数组。 tf.add(a, b, name='add') 这行代码在运行时并不会得到结果，而是一个结果的引用，是一个张量的结构，包含三个属性 name、shape、dtype，name 仅仅是一个节点的名称；shape 是张量的维度，这个是一维的，长度为 2，这个属性比较重要；dtype 是数据类型，每个张量有唯一的数据类型，不同张量之间的计算需要保证类型统一。

上面的例子就是对两个常量做加法，然后生成计算结果的引用。

tf 运行模型 — 会话

tf 的会话用来执行定义好的运算，会话用来管理运行过程中的所有资源，计算完成后会帮助回收资源，通过 with tf.Session() as sess: 这种方式会在 with 结束时自动关闭回收资源。

通过 tf.ConfigProto 可以配置类似并行线程数、GPU分配策略、运算超时时间等参数，将配置添加到 tf.Session 中创建会话。

向前传播算法

通过全连接网络结构介绍，一个神经元有多个输入和一个输出，输出是不同输入的加权和，不同的输入权重就是神经网络的参数，神经网络的优化就是优化参数取值的过程。全连接网络结构是指相邻两层之间任意两个节点之间都有连接。

向前传播算法需要的三部分信息：

第一部分从实体中取出特征向量作为输入。
第二部分是神经网络的连接结构，不同神经元之间的输入输出的连接关系。
第三部分是每个神经元中的参数。

在 tf 中通过变量（tf.Variable）来保存和更新神经网络中的参数。

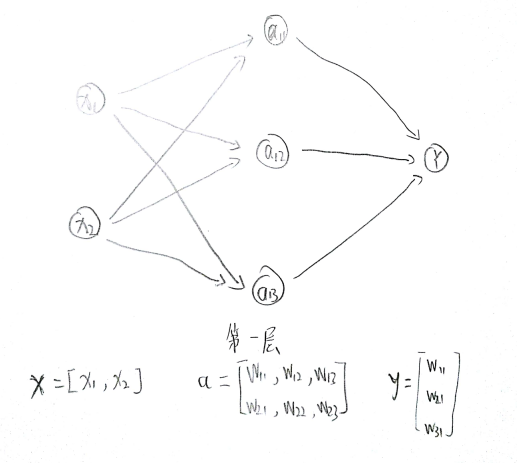
xiangqianchuanbo

import tensorflow as tf

# w1 是第一层，通过随机数生成一个 （2,3） 的矩阵
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
# w2 是第二层，通过随机石生成一个 （3,1） 的矩阵
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# x 是输入层，为一个 （1,2） 的矩阵
x = tf.placeholder(tf.float32, shape=(1, 2), name='input')

# 通过 tensorflow 提供的矩阵相乘算法计算
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

with tf.Session() as sess:
    # 这里初始化所有变量
    sess.run(tf.global_variables_initializer())
    # 通过 输入值 x 与 第一层的参数进行矩阵相乘，再与 第二层的参数进行矩阵相乘，实现神经网络的向前传播算法。
    print sess.run(y, feed_dict={x: [[0.7, 0.9]]})

[[ 3.95757794]]

AlfredWorkflow

发表于 2017-08-17

开发工程师常用工具箱

全局预览

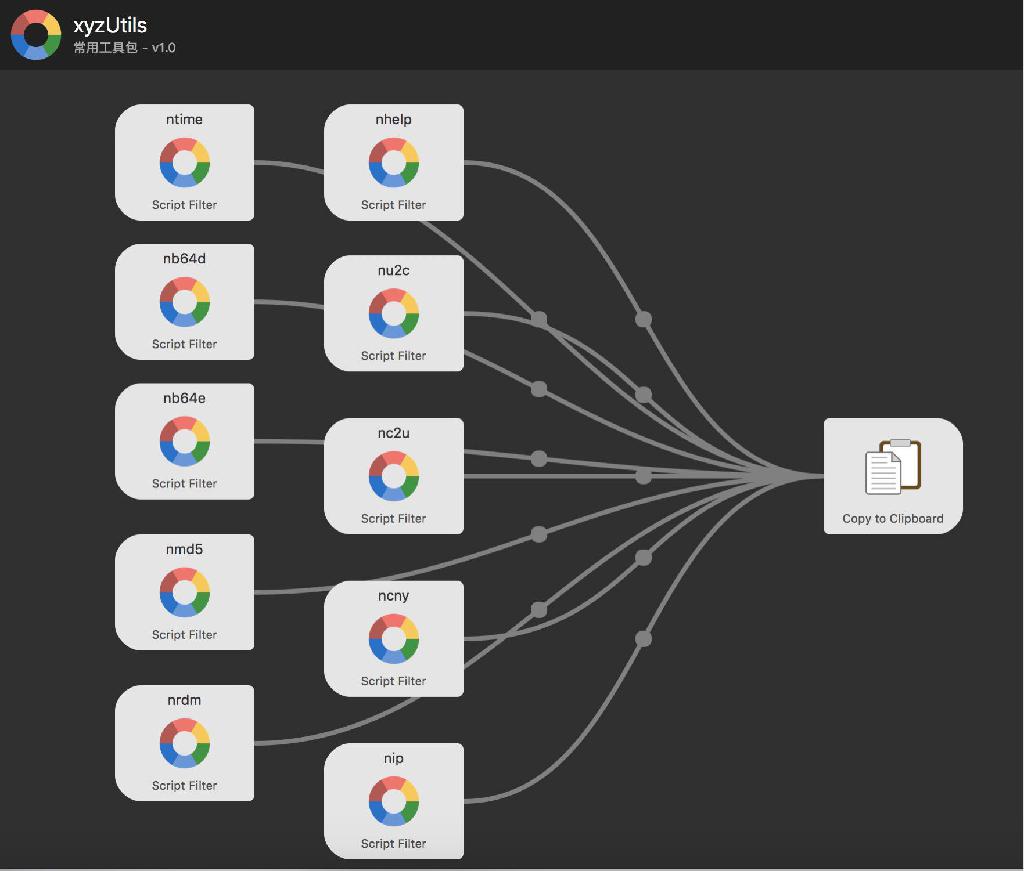
支持的命令

ntime 时间戳转换，支持标准时间格式与时间戳自动检测转换，回车复制结果到剪贴板
nb64d Base64 解码
nb64e Base64 编码
nmd5 MD5 生成
ncny 数字转人民币大写
nu2c Unicode 码转中文
nc2u 中文转 Unicode 码
nip IP 地址查询
nrdm 随机字符串生成，输入长度
nhelp 列出所有支持的命令

欢迎大家补充。

个人博客

知一的指纹

Github

Noogel’s github Alfred-Workflow

Update at 2017-08-17

Python字符串编码

发表于 2017-06-24

说道Python字符串编码处理会让很人头疼，下面介绍一些 Python 处理字符串编码的方式。

chardet 模块

chardet 主要用于编码识别

pip安装： sudo pip install chardet

官方地址： http://pypi.python.org/pypi/chardet

In [1]: import chardet

In [2]: import urllib

In [3]: test_data = urllib.urlopen('http://www.baidu.com/').read()

In [4]: chardet.detect(test_data)
Out[4]: {'confidence': 0.99, 'language': '', 'encoding': 'utf-8'}

In [5]: isinstance(test_data.decode('utf-8'), unicode)
Out[5]: True

In [6]: isinstance(test_data, unicode)
Out[6]: False

运行结果：
{'confidence': 0.99, 'language': '', 'encoding': 'utf-8'}
运行结果表示有 99% 的概率认为这段代码是 utf-8 编码方式。

对于大文件的编码识别，可以通过 UniversalDetector 部分读取进行检查。

In [1]: import urllib

In [2]: import chardet

In [3]: from chardet.universaldetector import UniversalDetector

In [4]: uso = urllib.urlopen('http://www.baidu.com/')
   ...: det = UniversalDetector()
   ...: for line in uso.readlines():
   ...:     det.feed(line)
   ...:     if det.done:
   ...:         break
   ...: det.close()
   ...: uso.close()
   ...: det.result
   ...:
Out[4]: {'confidence': 0.99, 'encoding': 'utf-8', 'language': ''}

运行结果：
{'confidence': 0.99, 'encoding': 'utf-8', 'language': ''}

Python 模块之 codecs

Mark未完

你的Ubuntu还可以这么美

发表于 2017-06-17

先上两张桌面和开发环境见下图

系统优化

更新源

更新前先设置源为aliyun的，国内访问速度快。

更新源

1 2	sudo apt-get update sudo apt-get upgrade

删除Amazon的链接

1	sudo apt-get remove unity-webapps-common

主题美化

先装 Unity 图形管理工具

1	sudo apt-get install unity-tweak-tool

然后安装 Flatabulous 主题

1
2
3

sudo add-apt-repository ppa:noobslab/themes
sudo apt-get update
sudo apt-get install flatabulous-theme

和配套图标

1
2
3

sudo add-apt-repository ppa:noobslab/icons
sudo apt-get update
sudo apt-get install ultra-flat-icons

更换操作如下图：

至此主题美化完成

System Load Indicator（系统状态指示器）

1
2
3

sudo add-apt-repository ppa:indicator-multiload/stable-daily
sudo apt-get update
sudo apt-get install indicator-multiload

微软雅黑

字体下载

1
2
3

tar zxvf YaHeiConsolas.tar.gz
sudo mv YaHeiConsolas.ttf /usr/share/fonts
sudo chmod 755 /usr/share/fonts/YaHeiConsolas.ttf

安装zsh

1
2
3

sudo apt-get install zsh
zsh --version
sudo chsh -s $(which zsh)

然后再重新注销登录就好了

必装软件

下面介绍的软件有一部分是通过 deb 文件安装的，具体安装方式见系统使用技巧。

系统软件

浏览器： Chrome
搜狗输入法： sougoupinyin
为知笔记： wiznote
系统状态指示器： System Load Indicator
SS你懂得： Shadowsocks-Qt5
Unity图形管理工具： unity tweak tool
图片编辑工具： gimp
思维导图： xmind
EPUB文件编辑： sigil
Linux下的Dash： zeal
Linux下Albert： albert
网易云音乐播放器
Robomongo

数据库及工具

mysql
mongodb
redis
MySQL Workbench

开发环境

Python IDE： Pycharm

命令行工具

zsh
oh-my-zsh
vim
git

系统使用技巧

DEB软件安装

安装命令

sudo dpkg -i xxx.deb

安装过程中可能会报缺少依赖的错，执行下面命令自动安装依赖

sudo apt-get install -f

再次执行安装命令

sudo dpkg -i xxx.deb

卸载不再依赖的包命令

sudo apt-get autoremove

未完待续，欢迎大家发送你的优化点到我的邮箱 noogel@163.com

Windows 效率工具包

发表于 2017-05-06

管理工具：Vstart 5.1

截图工具：FastStone Capture

定时关机：Easy定时关机

文本比较工具：Beyond Compare

FTP工具：FlashFXP

源代码格式：CoolFormat

SSH客户端：SecureCRT putty

文件搜索工具：Everything

翻译软件：QTranslate

局域网聊天:飞鸽传书

剪贴板增强：Ditto

数据恢复软件：Recover My Files

虚拟光驱：UltraISO

GIF录屏软件：licecap

PDF文件编辑工具：PDFEditor

音视频转换软件：FormatFactory

二维码生成软件：Psytec QR Code Editor

IP查询转换工具：纯真IP

破解软件：EWSA

OllyICE

VNCViewer

JAVA反编译：jd-gui

Android逆向助手

磁盘剩余空间查询：SpaceSniffer

键位映射工具：KeySwap

键盘测试工具：Keyboard Test Utility

GHO镜像浏览

磁盘分区软件：DiskGenius

系统镜像制作：老毛桃、晨枫U盘启动

BCD文件编辑：EasyBCD

win7激活软件、HEU_KMS_Activator

科学上网：ShadowsocksR

Spy4Win

任务管理器增强：System Explorer

关于Java的最初了解

发表于 2017-03-15

Apache Maven

Maven 是一个项目管理和构建自动化工具。但是对于我们程序员来说，我们最关心的是它的项目构建功能，它可以规定项目的文件结构，比如下面：

目录	目的
${basedir}	存放 pom.xml和所有的子目录
${basedir}/src/main/java	项目的 java源代码
${basedir}/src/main/resources	项目的资源，比如说 property文件
${basedir}/src/test/java	项目的测试类，比如说 JUnit代码
${basedir}/src/test/resources	测试使用的资源

Spring Boot

Spring Boot 是一个轻量级框架，Spring Boot 的目的是提供一组工具，以便快速构建容易配置的 Spring 应用程序。

Apache Tomcat

Tomcat是由Apache软件基金会下属的Jakarta项目开发的一个Servlet容器，实现了对Servlet和JavaServer Page（JSP）的支持，并提供了作为Web服务器的一些特有功能，如Tomcat管理和控制平台、安全域管理和Tomcat阀等。由于Tomcat本身也内含了一个HTTP服务器，它也可以被视作一个单独的Web服务器。Apache Tomcat包含了一个配置管理工具，也可以通过编辑XML格式的配置文件来进行配置。

Hibernate

是一种Java语言下的对象关系映射解决方案。Hibernate不仅负责从Java类到数据库表的映射（还包括从Java数据类型到SQL数据类型的映射），还提供了面向对象的数据查询检索机制，从而极大地缩短了手动处理SQL和JDBC上的开发时间。

Spring web MVC

框架提供了模型-视图-控制的体系结构和可以用来开发灵活、松散耦合的 web 应用程序的组件。MVC 模式导致了应用程序的不同方面(输入逻辑、业务逻辑和 UI 逻辑)的分离，同时提供了在这些元素之间的松散耦合。

结算开发中遇到的坑

发表于 2017-03-02

坑1：浮点数不精确性

1 2	In [1]: 0.1+0.1+0.1-0.3 Out[1]: 5.551115123125783e-17

解决办法：

1
2
3

In [2]: from decimal import Decimal
In [3]: Decimal('0.1') + Decimal('0.1') + Decimal('0.1') - Decimal('0.3')
Out[3]: Decimal('0.0')

坑2：Decimal使用问题

1 2	In [5]: Decimal(0.1) + Decimal(0.1) + Decimal(0.1) - Decimal(0.3) Out[5]: Decimal('2.775557561565156540423631668E-17')

解决办法：
参照坑1的解决办法，Decimal传入值需要str类型
更多用法查看：https://docs.python.org/2/library/decimal.html

坑3：四舍五入不准确问题

In [3]: '{:.2f}'.format(Decimal(str(1001.8250)))
Out[3]: '1001.82'
In [2]: Decimal('1001.8250').quantize(Decimal('0.01'))
Out[2]: Decimal('1001.82')
In [4]: round(2.55, 1)
Out[4]: 2.5

解决办法：
发现问题原因为在不能正确四舍五入的float数值中都是因为数据存储末位的.5被存储为.4999999…的形式，解决办法是在.5上加.1的值。

def exact_round(num, exp=2):
    """
    准确的四舍五入方法
    :param num: 数值
    :param exp: 保留精度
    :return:
    """
    str_num = str(num)
    dec_num = Decimal(str_num)
    exp_unit = Decimal('0.1') ** exp
    mini_unit = Decimal('0.1') ** (exp + 1)
    if dec_num % exp_unit == (5 * mini_unit):
        dec_num += mini_unit
    return Decimal(dec_num).quantize(exp_unit, rounding=ROUND_HALF_EVEN)

为了验证这个方法写了个测试脚本：

#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
摘    要: exact_round.py
创 建 者: abc
创建日期: 2017-01-05
"""
__author__ = "abc"

from decimal import Decimal, ROUND_HALF_EVEN


def exact_round(num, exp=2):
    """
    准确的四舍五入方法
    :param num: 数值
    :param exp: 保留精度
    :return:
    """
    str_num = str(num)
    dec_num = Decimal(str_num)
    exp_unit = Decimal('0.1') ** exp
    mini_unit = Decimal('0.1') ** (exp + 1)
    raw_num = dec_num
    if dec_num % exp_unit == (5 * mini_unit):
        dec_num += mini_unit
    raw_result = Decimal(raw_num).quantize(exp_unit, rounding=ROUND_HALF_EVEN)
    result = Decimal(dec_num).quantize(exp_unit, rounding=ROUND_HALF_EVEN)
    if result != raw_result:
        print "raw:round({}, {}) = > {}; fixed: round({}, {}) => {}".format(
            raw_num, exp, raw_result,
            dec_num, exp, result
        )
    return result
 
if __name__ == "__main__":
    val = 900.0000
    while val < 1001.8600:
        for exp in range(0, 6):
            exact_round(val, exp=exp)
        val += 0.0005

脚本中我们将被修正过的数据打印出来，发现被打印出来的都是四舍五入不正确的数值，经过方法处理可以保证准确的输出。

因为我们的测试只是覆盖了部分的数值，精度深度也只到到了6位，也不能保证说方法没有问题。
后来询问了在银行做开发的朋友，他们对于数据的计算都是在数据库的存储过程中运算的，并对上面坑中的数值放到数据库中做四舍五入发现确实没有问题。

于是我将这个方法做的运算与数据库的运算结果做对比写了测试脚本。

#!/usr/bin/python
# -*- coding: utf-8 -*-
"""
摘    要: test_db_round.py
创 建 者: abc
创建日期: 2017-01-06
"""
__author__ = "abc"
import os
import sys

sys.path.append(os.path.dirname(os.path.split(os.path.realpath(__file__))[0]))

from lib.utils import exact_round
from model import Model
 
def test_db_round(val, exp):
    """
    test_db_round
    :return:
    """
    sql = "SELECT round({}, {}) as val".format(str(val), exp)
    db_round = Model().raw(sql)[0]["val"]
    exa_round = exact_round(val, exp)
    if str(db_round) != str(exa_round):
        print "db:{}; ex:{}".format(str(db_round), str(exa_round))
 
if __name__ == "__main__":
    val = 900.0000
    while val < 1001.8600:
        for exp in range(0, 6):
            test_db_round(val, exp=exp)
        val += 0.0005

经过测试后发现没有数据被打印出，证明在测试范围内Python方法和数据库的运算结果没有差异。

关于浮点数不精确性的事情相信学过计算机组成原理这门课程的都明白，这里不再赘述，放个链接：
从如何判断浮点数是否等于0说起——浮点数的机器级表示

话说为什么要在Python中做财务相关运算呢，可能最初开发这个系统的人缺乏这方面的经验，然后通过扩展精度保留位数来解决这个问题的，但终究在做四舍五入时可能产生1分的差异。
既然发现这个问题，本着眼里不揉沙子的态度，快速的解决方案是在Python中替换原来的四舍五入函数，长期策略是逐步将计算过程挪到数据库通过存储过程来实现。

Tensorflow学习

发表于 2017-02-09

1 2	import tensorflow as tf import numpy as np

# 例子1

x_data = np.random.rand(100).astype(np.float32)
y_data = x_data*0.4 + 0.9

weight = tf.Variable(tf.random_uniform([1], -0.1, 1.0))
biases = tf.Variable(tf.zeros([1]))

y = weight * x_data + biases

loss = tf.reduce_mean(tf.square(y - y_data))
# 误差传递方法是梯度下降法
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
# 始化所有之前定义的Variable
init = tf.initialize_all_variables()

sess = tf.Session()
sess.run(init)

for step in range(200):
    sess.run(train)
    if step % 20 == 0:
        print step, sess.run(weight), sess.run(biases)

WARNING:tensorflow:From <ipython-input-3-3c832ce985bb>:16 in <module>.: initialize_all_variables (from tensorflow.python.ops.variables) is deprecated and will be removed after 2017-03-02.
Instructions for updating:
Use `tf.global_variables_initializer` instead.
0 [ 0.8605063] [ 0.92711782]
20 [ 0.49690402] [ 0.8437199]
40 [ 0.42823532] [ 0.88360143]
60 [ 0.40822706] [ 0.89522189]
80 [ 0.40239716] [ 0.89860773]
100 [ 0.40069851] [ 0.89959431]
120 [ 0.40020356] [ 0.89988178]
140 [ 0.40005937] [ 0.89996552]
160 [ 0.40001735] [ 0.8999899]
180 [ 0.40000507] [ 0.89999706]

# 例子2

matrix1 = tf.constant([[3,3]])
matrix2 = tf.constant([[2], [2]])

product = tf.matmul(matrix1, matrix2)

# method 1
sess = tf.Session()
result = sess.run(product)
print result
sess.close()

# method 2
with tf.Session() as sess:
    result = sess.run(product)
    print result

[[12]]
[[12]]

# Variable变量
import tensorflow as tf
state = tf.Variable(0, name='counter')

# 定义常量1
one = tf.constant(1)

# 定义加法步骤 (注: 此步并没有直接计算)
new_value = tf.add(state, one)

# 将 State 更新成 new_value
update = tf.assign(state, new_value)

init = tf.initialize_all_variables()

with tf.Session() as sess:
    sess.run(init)
    for _ in range(3):
        sess.run(update)
        print sess.run(state)

WARNING:tensorflow:From <ipython-input-12-816914535228>:14 in <module>.: initialize_all_variables (from tensorflow.python.ops.variables) is deprecated and will be removed after 2017-03-02.
Instructions for updating:
Use `tf.global_variables_initializer` instead.
1
2
3

# placeholder 传入值

# 预定义传入值
input1 = tf.placeholder(tf.float32)
input2 = tf.placeholder(tf.float32)

output = tf.mul(input1, input2)

with tf.Session() as sess:
    # feed_dict传入实际值
    print sess.run(output, feed_dict={input1:[7.], input2: [2.]})

[ 14.]

Activation Functions 激励函数 tf.nn

# 添加神经层 add_layer

def add_layer(inputs, in_size, out_size, activation_function=None):
    # 在生成初始参数时，随机变量(normal distribution)会比全部为0要好很多
    # 所以我们这里的weights为一个in_size行, out_size列的随机变量矩阵。
    weights = tf.Variable(tf.random_normal([in_size, out_size]))
    # biases的推荐值不为0，所以我们这里是在0向量的基础上又加了0.1
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    wx_plus_b = tf.matmul(inputs, weights) + biases
    if activation_function is None:
        outputs = wx_plus_b
    else:
        outputs = activation_function(wx_plus_b)
    return outputs


# 建造神经网络
x_data = np.linspace(-1, 1, 300)[:, np.newaxis]

# 方差0.05, x_data.shape数据形式
noise = np.random.normal(0, 0.05, x_data.shape)
# x_data 二次方
y_data = np.square(x_data) - 0.5 + noise

# 输入层 -> 隐藏层 -> 输出层

# 输入值
xs = tf.placeholder(tf.float32, [None, 1])
ys = tf.placeholder(tf.float32, [None, 1])
# 定义隐藏层 1 输入层神经元数量， 输出层神经元数量，隐藏层神经元数量
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)
# 定义输出层
prediction = add_layer(l1, 10, 1, activation_function=None)

# 预测误差 二者差的平方和再求平均值
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices=[1]))

# 提供学习效率0.1，通常小于1， 最小化误差
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

init = tf.initialize_all_variables()

sess = tf.Session()
sess.run(init)

for i in range(1000):
    sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
    if i % 50 == 0:
        # 输出误差
        print sess.run(loss, feed_dict={xs: x_data, ys: y_data})

WARNING:tensorflow:From <ipython-input-36-245eb01b43f9>:41 in <module>.: initialize_all_variables (from tensorflow.python.ops.variables) is deprecated and will be removed after 2017-03-02.
Instructions for updating:
Use `tf.global_variables_initializer` instead.
0.295339
0.00607488
0.00473904
0.00429677
0.00412784
0.0040373
0.0039907
0.00395235
0.00391656
0.00388327
0.00385458
0.0038216
0.00378461
0.00374649
0.00369835
0.00366241
0.00363534
0.00361383
0.0035907
0.00357239

# 结果可视化
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(1,1,1)
ax.scatter(x_data, y_data)
# plt.ion()
plt.show()

png

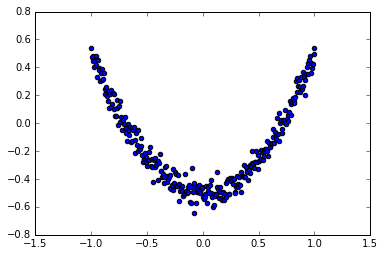
# 展示每一步的学习结果
with tf.Session() as sess:
    sess.run(init)
    for i in range(1000):
        sess.run(train_step, feed_dict={xs: x_data, ys: y_data})
        if i % 100 == 0:
            # 输出误差
            # print sess.run(loss, feed_dict={xs: x_data, ys: y_data})
            prediction_value = sess.run(prediction, feed_dict={xs: x_data})
            fig = plt.figure()
            ax = fig.add_subplot(1,1,1)
            ax.scatter(x_data, y_data)
            try:
                # 去除原来的线
                ax.lines.remove(lines[0])
            except:
                pass
            # 画线
            lines = ax.plot(x_data, prediction_value, 'r-', lw=5)
            # 暂停一个时间
            plt.show()

png

1
2
3

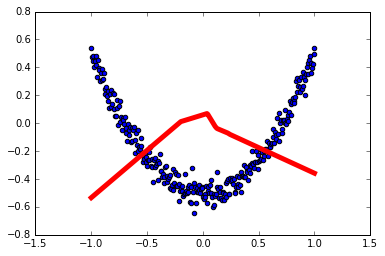
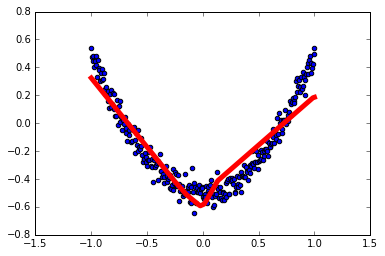
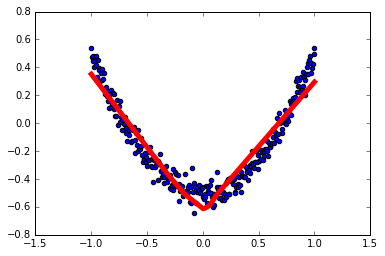
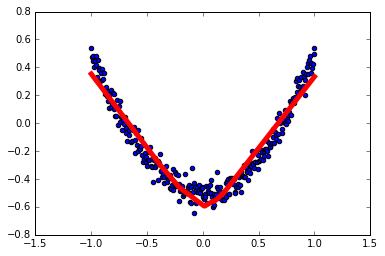
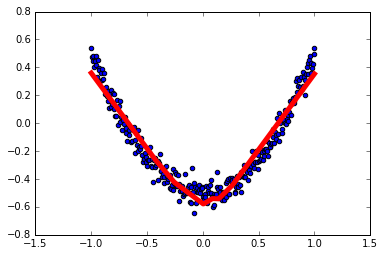
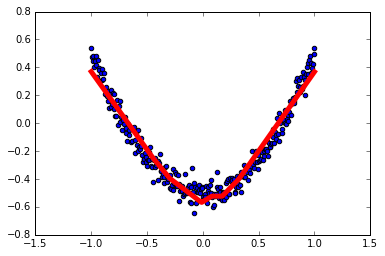
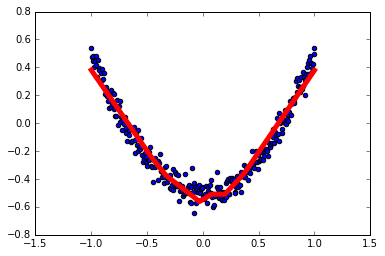
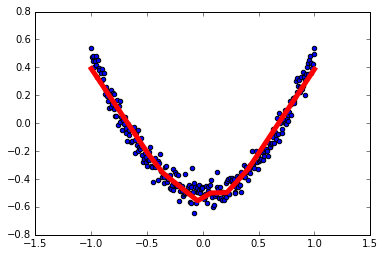
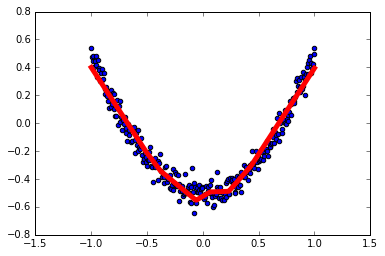
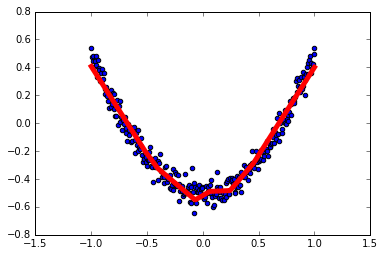
# Optimizer 优化器

# GradientDescentOptimizer最基本的一种

反向传播算法

激活函数去线性化

损失函数

反向传播算法

过拟合问题

滑动平均模型

人工智能、机器学习和深度学习之间的关系？

深度学习的发展历程

TensorFlow 学起来

tf 计算模型 — 计算图

tf 数据模型 — 张量

tf 运行模型 — 会话

向前传播算法

全局预览

支持的命令

欢迎大家补充。

个人博客

Github

chardet 模块

Python 模块之 codecs

系统优化

更新源

删除Amazon的链接

主题美化

System Load Indicator（系统状态指示器）

微软雅黑

安装zsh

必装软件

系统软件

数据库及工具

开发环境

命令行工具

系统使用技巧

DEB软件安装

卸载不再依赖的包 命令

Apache Maven

Spring Boot

Apache Tomcat

Hibernate

Spring web MVC

Activation Functions 激励函数 tf.nn

卸载不再依赖的包命令